Interpreting extreme weather statistics.

Why scientists must use caution when interpreting statistical outlier events in the weather and attributing them to anthropogenic climate change.

Extreme weather statistics…

Interpreting extreme weather statistics requires a high degree of caution due to the complex nature of weather patterns and the numerous variables that influence these events. Weather is inherently variable and unpredictable in its shorter-term fluctuations. While specific general patterns may appear to hold over brief periods, these patterns may not necessarily persist over longer periods. Therefore, a few years of extreme weather events might not be indicative of a long-term trend.

Additionally, extreme weather events are statistically rare, occurring at the tails of the distribution of weather phenomena. As such, a single additional event can significantly change calculated probabilities, rendering the statistics potentially misleading. It's also important to understand that the definition of what constitutes an 'extreme' event can change over time, influenced by improvements in detection capabilities and shifting scientific consensus.

There's also a necessary caution when linking weather events to climate change. While some climate scientists predict that climate change will increase the frequency and severity of some extreme weather events, attributing a specific weather event to climate change is a complex task. Just because an extreme event has occurred, it does not conclusively mean it was caused by climate change. Conversely, a period lacking in extreme events does not suggest that climate change isn't occurring.

Data quality and its geographical coverage present another challenge. Weather data, especially older records or those from less developed regions, may be of varying quality. Inconsistent data can make it difficult to distinguish genuine trends from anomalies created by the data collection process. Furthermore, statistical considerations come into play; weather phenomena often do not follow simple statistical patterns, such as the Gaussian distribution, complicating analysis.

What is the Gaussian distribution?

A Gaussian distribution, also known as a normal distribution, is a type of statistical distribution where observations are most likely to occur around the mean. It is symmetric and follows a bell-shaped curve, also known as a Gaussian function.

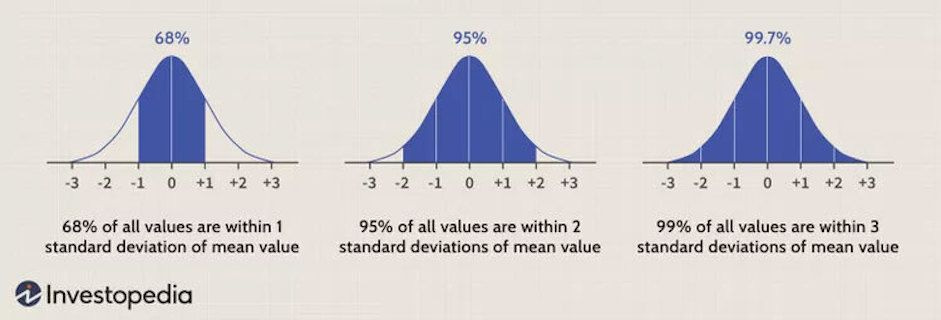
The distribution is defined by two parameters: the mean (µ) and the standard deviation (σ). The mean indicates the center of the distribution where the peak of the bell curve resides, and the standard deviation measures the spread or dispersion of the data.

In a normal distribution:

• About 68% of the data falls within one standard deviation of the mean.

• About 95% falls within two standard deviations.

• About 99.7% falls within three standard deviations.

This is often referred to as the 68-95-99.7 rule or the empirical rule.

The formula for a Gaussian distribution function is:

f(x) = (1/σ√(2π)) * e^(-(x-µ)²/2σ²)

Where:

• x is the point in the distribution you're interested in

• µ is the mean

• σ is the standard deviation

• e is the base of the natural logarithm, approximately equal to 2.71828

• π is Pi, approximately equal to 3.14159

The Gaussian distribution is widely used in statistics and the natural and social sciences as a simple model for complex random variables. It's often a good approximation for real-world data, thanks to the Central Limit Theorem, which states that the sum of many independent random variables tends towards a normal distribution, given certain conditions.

Source: https://www.investopedia.com/terms/n/normaldistribution.asp

Gaussian distribution in climate science…

Many things in nature approximate a Gaussian distribution, also known as a normal distribution or bell curve. This is due to the Central Limit Theorem, which states that the sum of a large number of independent and identically distributed (i.i.d.) random variables, each with finite mean and variance, will approximately follow a normal distribution, regardless of the shape of the original distribution.

For example, measurements of physical characteristics often follow a normal distribution. This includes things like the heights or weights of a large group of people, the size of trees in a forest, or the length of a certain type of animal. Errors or residuals in scientific experiments also often follow a normal distribution.

However, not everything in nature follows a normal distribution. Some things follow different distributions. For instance:

• The sizes of cities in many countries follow a distribution known as Zipf's law, which is a type of power law distribution.

• The magnitude of earthquakes follows the Gutenberg-Richter law, another type of power law distribution.

• The distribution of species in biological communities often follows a lognormal distribution.

• The distribution of income in many societies follows a Pareto distribution, which is heavy-tailed.

There are also a lot of natural phenomena where the distribution is not known or is complex and multi-modal (having multiple peaks).

A study published in the Journal of Climate titled, “Need for Caution in Interpreting Extreme Weather Statistics” states:

Given the reality of anthropogenic global warming, it is tempting to seek an anthropogenic component in any recent change in the statistics of extreme weather. This paper cautions that such efforts may, however, lead to wrong conclusions if the distinctively skewed and heavy-tailed aspects of the probability distributions of daily weather anomalies are ignored or misrepresented. Departures of several standard deviations from the mean, although rare, are far more common in such a distinctively non-Gaussian world than they are in a Gaussian world. This further complicates the problem of detecting changes in tail probabilities from historical records of limited length and accuracy.

Observing new statistical outlier events in the era of real-time climate monitoring…